Условие задачи

Ключ к решению:

Если исполнитель «черепашка» совершает два предопределенных действия: перемещение вперед на заданное расстояние и поворот направо на заданный угол, то при определенном количестве повторов, «черепашка» вернется в ту точку из которой началось движение, если число, которое получается при делении 360 на величину угла, целое. Чем больше угол поворота, тем за меньшее количество повторов «черепашка» вернется в исходную точку. Если угол поворота равен 1, замкнутая фигура будет иметь 360 углов.

Сумма внешних углов правильного многоугольника - 360 градусов.

Очевидно, что величина угла и количество повторов взаимосвязаны.

Эта взаимосвязь становиться ясна, если мы поймем, что в момент возвращения «черепашки» в исходную точку, она совершает суммарный поворот на 360 градусов и каждый повтор есть равная угловая часть этой суммы.

Пусть X - количество повторов, A - величина внешнего угла поворота,- искомая формула: X = 360/A или A = 360/X

Проверим на простых упражнениях:

С целью внести дополнительную сложность в нахождение ответа, задача может быть информационно усложнена, например, так:

Но сути решения это не меняет, просто «Черепашка» «обойдет» нарисованный квадрат несколько раз.

Прежде, чем решить приведенную выше задачу, пройдите ряд простых заданий:

• вариант 1 - преобразуйте квадрат в треугольник, в шестиугольник и ромб
• вариант 2 - внесите изменения в код так, чтобы 2 квадрата касались вершинами и были расположены напротив друг друга
• вариант 3 - напишите программу, которая нарисует, изображенную на рисунке фигуру:

Необычный восьмиугольник

repeat 8[
 repeat 8[
   forward 50
   turn 45
 ]
turn 45
]

• Орнамент

Если Вы справились со всеми заданиями и у Вас осталось время:tangram

Исходный код:

terrapin_gia_a6.zip

Если Вы повторяете материал, после того, как ознакомились с основными командами языка программирования Python, используйте для проверки решения поставленных задач, среду исполнителя:

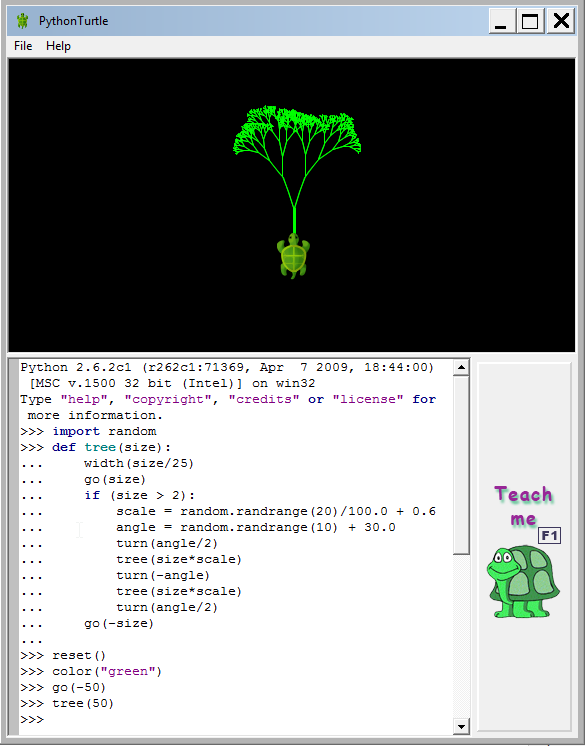
Python Turtle («Черепашка») http://pythonturtle.org/ - Учебный игровой тренажер, позволяющий в деятельностной игровой форме осваивать принципы алгоритмизации, визуализировать действия исполнителя, интерпретирующего программный код, написанный на языке Python. На рисунке представлен пример, моделирующий вариант решения одной из задач ГИА:

Полагаю Вас не должно «испутать» то, что имена переменных на данном примере не соответствуют именам переменных в предыдущих примерах и обозначают: n - количество повторов, x - расстояние, которое преодолевает «Черепашка» за одно действие, а угол программа вычисляет автоматически.

Напишите алгоритм, позволяющий вернуться «Черепашке» в исходную точку, повторно совершая два предопределенных действия (движение вперед и поворот), если известно, что

x = 30 # расстояние при движении вперед
a = 40 # угол при повороте направо
# допишите программный код 
# Внимание! Количество повторов программа должна вычислить автоматически.

Если Вы уже имели дело с блок-схемами, перейдите в программу lucidchart и составьте блок-схему алгоритма программы, следуя которой, исполнитель «Черепашка» рисует правильные многоугольники (для первого варианта: известно количество повторов).

Сравните результат, который у Вас получился с данным результатом (если желаете оценить свой уровень - заранее не смотрите подсказку).

Фрактальная графика (дерево)

import random
def tree(size):
	width(size/25)
	go(size)
	if (size > 2):
		scale = random.randrange(20)/100.0 + 0.6
		angle = random.randrange(10) + 30.0
		turn(angle/2)
		tree(size*scale)
		turn(-angle)
		tree(size*scale)
		turn(angle/2)
	go(-size)
 
reset()
color("green")
go(-50)
tree(50)

from turtle import *
import random
def tree(size):
	width(size/25 + 1)
	fd(size)
	if (size > 2):
		scale = random.randrange(11)/50.0 + 0.4
		angle = random.randrange(5) + 40.0
		rt(angle/2)
		tree(size*scale)
		lt(angle)
		tree(size*scale)
		rt(angle/2)
	fd(-size)
 
reset()
lt(90)
color("green")
fd(-70)
tree(70)